Brillouin Scattering Database

Christoffel Equations for Crystal Systems

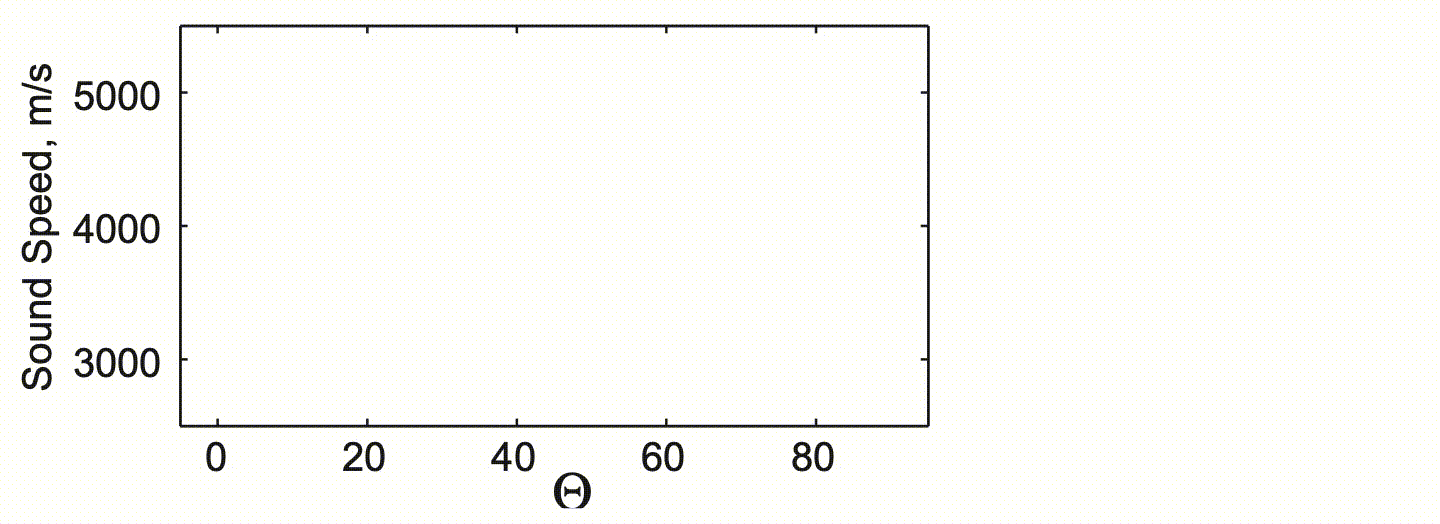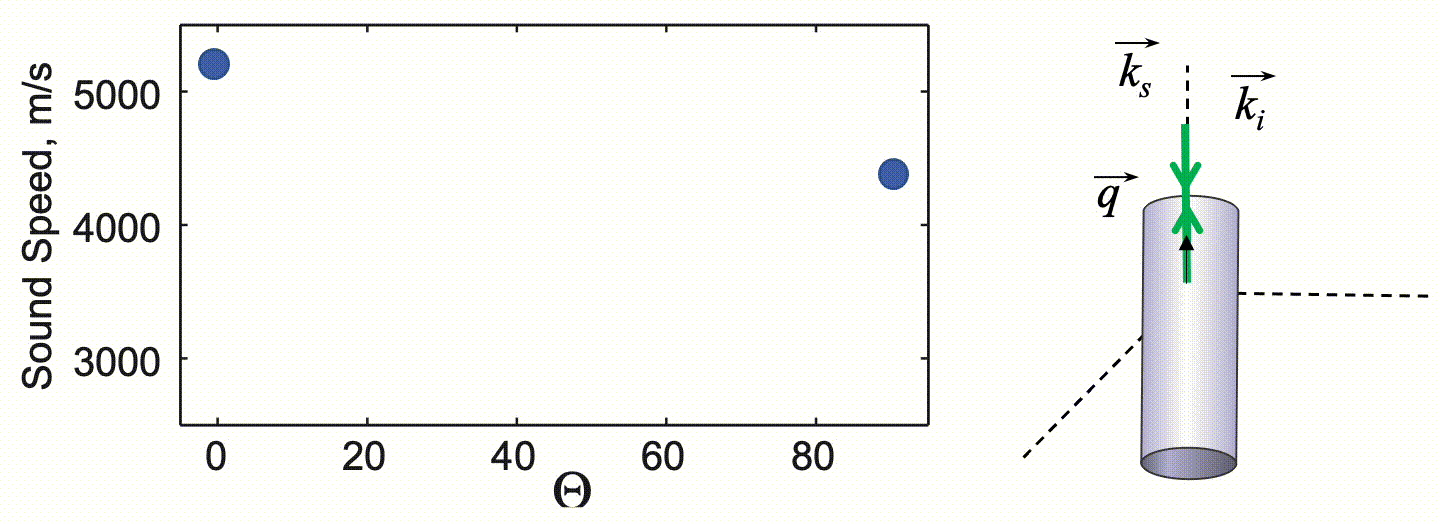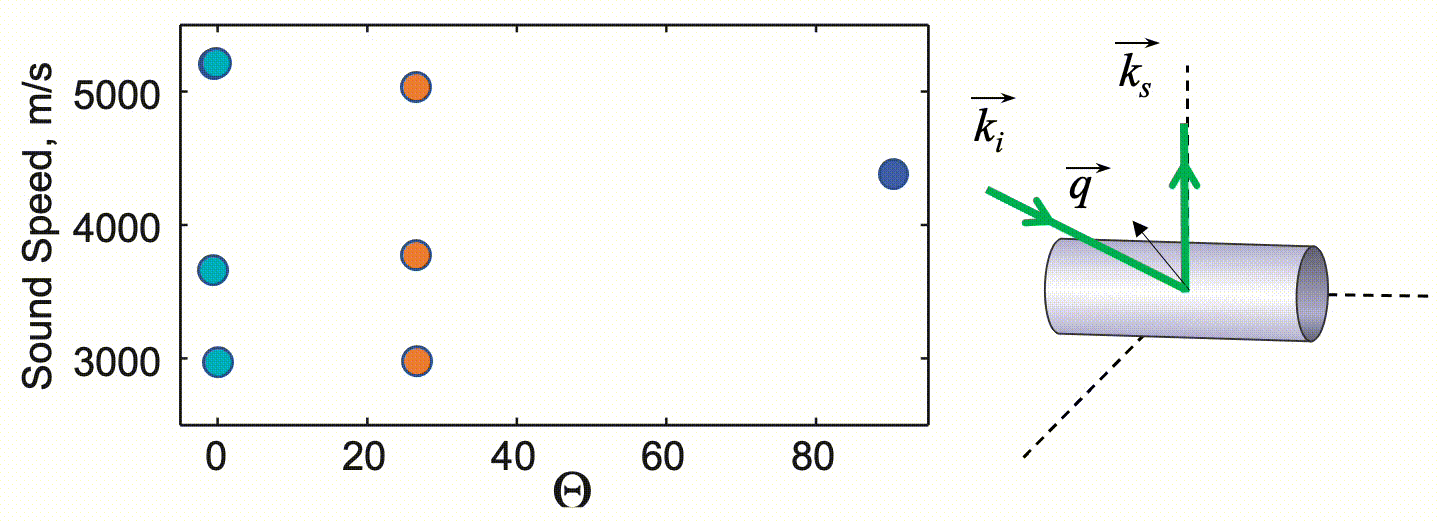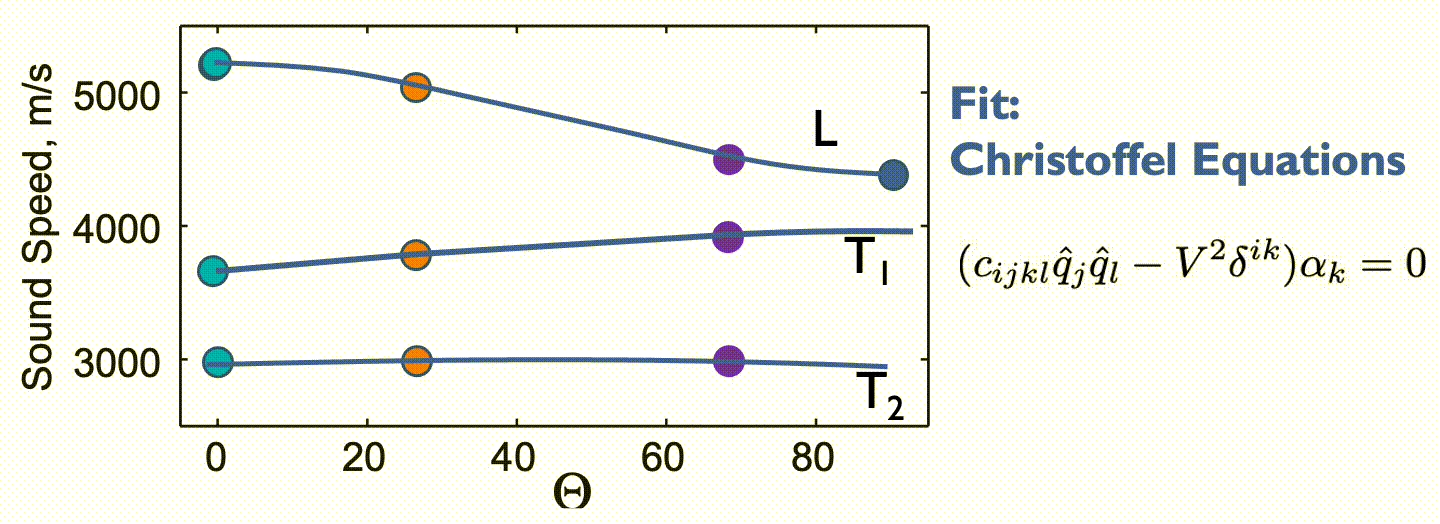
Solutions of the Christoffel Equations give the elastic stiffness tensor when the sound velocity or frequency shift of the Brillouin scattered light has been measured as a function of angular propogation of the phonon wavevector in the sample.

\(c_{ij}\) are the elastic stiffnesses; \(\theta\) is the angular direction of phonon wave-vector propogation. This should be assigned with respect to a crystallographic direction (e.g. with respect to the [001] direction); \(\rho\) is the crystal density

Tetragonal

\[ \nu_1 = \sqrt{\frac{A_1 \sin^2 \theta}{2\rho} + \frac{c_{44} \cos^2 \theta}{\rho}} \] \[ \nu_{0,2} = \sqrt{\frac{(A_2+ c_{44}) \sin^2 \theta + A_3 \cos^2 \theta \pm \{ [(A_2-c_{44}) \sin^2 \theta - A_4 \cos^2 \theta]^2 +(2A_5 \sin \theta \cos \theta)^2 \} ^{1/2}}{2\rho}} \] where: \[ A_1 = c_{11} - c_{12}\\ A_2 = \frac{1}{2}(c_{11}+c_{12}) + c_{66} \\ A_3 = c_{33} + c_{44} \\ A_4 = c_{33} - c_{44} \\ A_5 = c_{13} + c_{44} \]

Cubic

\(\vec{k}\) lies in the (001) plane at an angle \(\theta\) to the \( x \) axis: \[ V_{1} = \sqrt{\frac{c_{44}}{\rho}} \] \[ V_{0,2} = \sqrt{ \frac{ \frac{1}{2} \{ (c_{11}+c_{44}) \pm [(c_{11}-c_{44})^2-4K(c_{11}+c_{12})\cos^2 \theta \sin^2 \theta ]^{1/2} \} }{\rho}} \] \(\vec{k}\) lies in the \( (0\bar{1}1) \) plane at an angle \(\theta\) to the \( x \) axis: \[ V_{0,1} = \sqrt{ \frac{ \frac{1}{4}\ \{ (c_{11}+c_{12}+4c_{44}) + K \cos^2 \theta \pm [(c_{11}+c_{12})^2 - K(6c_{11}+14c_{12}+8c_{44})\cos^2 \theta + K(9c_{11}+15c_{12}+6c_{44})\cos^4 \theta]^{1/2} }{\rho}} \] \[ V_{2} = \sqrt{\frac{ \frac{1}{2} [(c_{11}-c_{12})-K\cos^2 \theta ]}{\rho}} \]

where for all cases: \[ K = c_{11} - c_{12}-2c_{44} \]

Hexagonal, Transversely isotropic, or Fiber Symmetry

\[ V_{L, T_1} = \frac{c_{11} \sin^2 \theta + c_{33} \cos^2 \theta + c_{44} \pm \sqrt{ [(c_{11}-c_{44})\sin^2 \theta + ( c_{44} - c_{33}) \cos^2 \theta]^2 + 4(c_{13} + c_{44})^2 \sin^2 \theta \cos^2 \theta}}{2\rho} \] \[ V_{T_2} = \sqrt{ \frac{c_{66} \sin^2 \theta + c_{44} \cos^2 \theta}{\rho}} \]

Hexagonal or Fiber Symmetry with \( c_{44} = c_{66} \)

\[ V_{L} = \sqrt{\frac{c_{11} \sin^2 \theta + c_{33} \cos^2 \theta + c_{44} + \sqrt{ [(c_{44}-c_{11})\sin^2 \theta + ( c_{33} - c_{44}) \cos^2 \theta]^2 + (c_{13} + c_{44})^2 \sin^2 2\theta}}{2\rho}} \] \[ V_{T_1} = \sqrt{\frac{c_{11} \sin^2 \theta + c_{33} \cos^2 \theta + c_{44} - \sqrt{ [(c_{44}-c_{11})\sin^2 \theta + ( c_{33} - c_{44}) \cos^2 \theta]^2 + (c_{13} + c_{44})^2 \sin^2 2\theta}}{2\rho}} \] \[ V_{T_2} = \sqrt{ \frac{c_{44}}{\rho}} \]

Adapted from Speziale et al. Biophysical Journal, 85, 3202-3213 (2003)

Auld, B.A.: Acoustic Fields and Waves in Solids, Artech House, Boston (1985)

Every, A.G. Physical Review Letters, 42, 1065 (1979)

Cusack, S., Miller, A. Journal of Molecular Biology, 135, 39-51 (1979)

Koski, K.J. et al. Nature Materials, 12, 262-7 (2013)