Isotropic elasticity: Longitudinal Modulus and Young's Modulus

An interesting elastic constant designation has arisen in recent years in Brillouin scattering called the "Longitudinal Modulus". Below is an explaination as to how this relates to the Young's modulus in an isotropic system.

Assuming an isotropic, elastic system, the stiffness tensor is given by: \[ \begin{eqnarray} c_{ij} = \left[ \begin{array}{cccccc} c_{11} & c_{12} & c_{12} & 0 & 0 & 0 \\ c_{12} & c_{11} & c_{12} & 0 & 0 & 0\\ c_{12} & c_{12} & c_{11} & 0 & 0 & 0\\ 0 & 0 & 0 & c_{44} & 0 & 0\\ 0 & 0 & 0 & 0 & c_{44} & 0\\ 0 & 0 & 0 & 0 & 0 & c_{44} \end{array} \right] = \left[ \begin{array}{cccccc} c_{11} & c_{12} & c_{12} & 0 & 0 & 0 \\ c_{12} & c_{11} & c_{12} & 0 & 0 & 0\\ c_{12} & c_{12} & c_{11} & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{c_{11}-c_{12}}{2} & 0 & 0\\ 0 & 0 & 0 & 0 &\frac{c_{11}-c_{12}}{2} & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{c_{11}-c_{12}}{2} \end{array} \right] \end{eqnarray} \]

where \( c_{44} = \frac{1}{2} \left(c_{11}-c_{12}\right) \)

Therefore, isotropic systems only have two stiffnesses: \( c_{11} \) and \( c_{12} \)

The Longitudinal Modulus ( \( LM \) ), as referred to in a Brillouin scattering experiment is the measurement of the stiffness from the longitudinal acoustic mode. In an isotropic system, it is simply one stiffness tensor element: \( c_{11} \)

\[ LM = c_{11} \]

To get \(c_{12}\), it is necessary to measure a transverse mode and get the transverse modulus \( c_{44} \). In a backscattering experiment of which most current Brillouin experiments are preferentially performed due to microscope use, symmetry forbids transverse peaks show up. So Transverse modes have to be measured using another scattering geometry. Again, this transverse mode corresponds to \(c_{44}\) which can be related to \(c_{12}\) by the equations above.

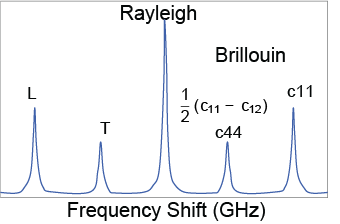
The sound velocity is related to the stiffness (where ij is 11 or 44 in an isotropic case) and density \( \rho \) via the Newton equation: \[ V = \sqrt{ \frac{c_{ij}}{\rho} } \] Brillouin gives a frequency shift ( \( \nu \) ) which can be converted into a sound velocity by the equation: \[ V = \frac{\lambda_o |\Delta \nu|}{2 n \sin \left( \frac{\Theta}{2} \right)} \] Sound Velocity equals sound velocity so this means that Brillouin scattering directly measures stiffness if the density is known. \[ c_{ij} = \rho \left( \frac{\lambda_o \Delta \nu }{2 n \sin \frac{\Theta}{2}} \right)^2 \]

How does this relate to Young's Modulus

An issue arises within the Brillouin literature with the use of "Longitudinal Modulus" and Young's modulus. A Longitudinal Modulus is a stiffness. The relationship to Young's modulus ( \( E \) ), shear modulus ( \( G \) ), or Bulk modulus ( \(B\) ) is made through combinations of the other stiffness element or rather, the transverse modulus as it would be called in keeping with this designation.

So if you measure \( c_{11} \) or \( c_{12} \), how does that related to the Young's modulus \( Y \) and Poisson's Ratio \( \sigma \)? \[ c_{11} = LM = \frac{Y(1-\sigma)}{(1+\sigma)(1-2\sigma)} \] \[ c_{12} = \frac{\sigma Y}{(1+\sigma)(1-2\sigma)} \] \[ c_{44} = G = \frac{Y}{2(1+\sigma)} \] Note how the Longitudinal modulus isn't the Young's modulus but is some combination of the Young's modulus and the Poisson's ratio.

What is the Young's Modulus in an isotropic elastic system? \[ Y = \frac{3 c_{12} c_{44} + 2 c_{44}^2}{c_{12} + c_{44}} = \frac{(c_{11}-c_{12})(c_{11}+2c_{12})}{c_{11}+c_{12}} \] From the constitutive relations, the Young's modulus is a combination of \( c_{11} \) and \( c_{12} \). It is not simply \( c_{11} \) nor is it simply the Longitudinal modulus. This is where a lot of mistakes are being made in the Brillouin literature. The rest of the mechanical constants can be calculated from the stiffnesses as follows:

Shear Modulus: \[ G = c_{44} \] Bulk Modulus: \[ B = \frac{1}{3}\left(c_{11}+2c_{12}\right) \] Poisson's Ratio: \[ \sigma = \frac{c_{12}}{c_{11}+c_{12}} \] And it follows that the Young's modulus is related to the Bulk modulus by \[ Y = \frac{9BG}{(3B+G)} \]

A very odd debate has apparently arisen in Brillouin spectroscopy where the claim is made that water content not stiffness dictates Brillouin scattering. This is an odd dichotomy. Mixture content determines stiffness; who cares what is in the mix. Elastic isotropic systems are best demonstrated by the Rules of Mixtures as shown in the figure below. The Rules of Mixtures is that as one component is added to make a material stiffer or softer, the stiffness should behave approximately linearly (with of course real world implications that always bend the curve). This type of rule comes in handy when mixing cements, adding water to jello (like all these biological phantoms), adding lead into glass, etc... There are, of course, exceptions to the rule of mixtures but in an isotropic linear elastic system, that should not be encountered. If it is, then it is more likely that the system is not linear elastic.

Final Considerations

Mechanical consideration: Brillouin is non contact and imparts a negligable displacement. It is linear and elastic. Mechanical perturbation is non-linear and non-elastic. The differences arise predominantly in the mechanical which has:

Mechanical Issues not found in Brillouin scattering
1. Nonlinearity in stress
2. Nonlinearity in strain
3. Viscoplasticity          

To accurately compare Brillouin scattering measurements to mechanical measurements, the deformation of the solid or materials in question must be taken into consideration.

Thermodynamic consideration:
Brillouin scattering is isentropic.

Mechanical perturbation is isothermal.